Dijkstra算法****
最后更新时间:2011.9.25
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
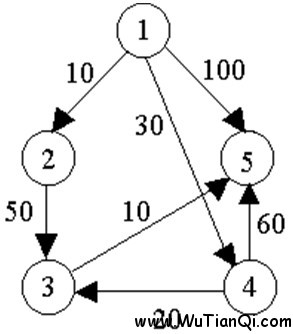
例如,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。
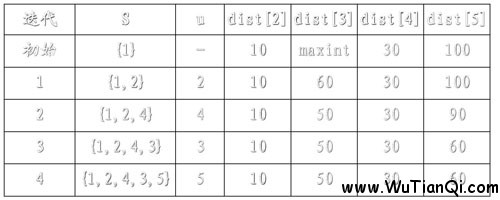
主题好好理解上图!
以下是具体的实现(C/C++):
/***************************************
* About: 有向图的Dijkstra算法实现
* Author: Tanky Woo
* Blog: www.WuTianQi.com
***************************************/
#include
using namespace std;
const int maxnum = 100;
const int maxint = 999999;
// 各数组都从下标1开始
int dist[maxnum]; // 表示当前点到源点的最短路径长度
int prev[maxnum]; // 记录当前点的前一个结点
int c[maxnum][maxnum]; // 记录图的两点间路径长度
int n, line; // 图的结点数和路径数
// n -- n nodes
// v -- the source node
// dist[] -- the distance from the ith node to the source node
// prev[] -- the previous node of the ith node
// c[][] -- every two nodes' distance
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
bool s[maxnum]; // 判断是否已存入该点到S集合中
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == maxint)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
// 注意是从第二个节点开始,第一个为源点
for(int i=2; i<=n; ++i)
{
int tmp = maxint;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]=1; --i)
if(i != 1)
cout << que[i] << " -> ";
else
cout << que[i] << endl;
}
int main()
{
freopen("input.txt", "r", stdin);
// 各数组都从下标1开始
// 输入结点数
cin >> n;
// 输入路径数
cin >> line;
int p, q, len; // 输入p, q两点及其路径长度
// 初始化c[][]为maxint
for(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
c[i][j] = maxint;
for(int i=1; i<=line; ++i)
{
cin >> p >> q >> len;
if(len < c[p][q]) // 有重边
{
c[p][q] = len; // p指向q
c[q][p] = len; // q指向p,这样表示无向图
}
}
for(int i=1; i<=n; ++i)
dist[i] = maxint;
for(int i=1; i<=n; ++i)
{
for(int j=1; j<=n; ++j)
printf("%8d", c[i][j]);
printf("\n");
}
Dijkstra(n, 1, dist, prev, c);
// 最短路径长度
cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
// 路径
cout << "源点到最后一个顶点的路径为: ";
searchPath(prev, 1, n);
}
输入数据: 5 7 1 2 10 1 4 30 1 5 100 2 3 50 3 5 10 4 3 20 4 5 60 输出数据: 999999 10 999999 30 100 10 999999 50 999999 999999 999999 50 999999 20 10 30 999999 20 999999 60 100 999999 10 60 999999 源点到最后一个顶点的最短路径长度: 60 源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5
最后给出两道题目练手,都是直接套用模版就OK的: 1.HDOJ 1874 畅通工程续 http://www.wutianqi.com/?p=1894
2.HDOJ 2544 最短路 http://www.wutianqi.com/?p=1892