这篇博客是从旧博客 WordPress 迁移过来,内容可能存在转换异常。
建议先看看前言:http://www.wutianqi.com/?p=2298
上一章总结是的堆排序算法,这一章同样是利用了堆这种数据结构,实现在是优先级队列。
根据堆分为最大堆,最小堆,所以优先级队列也可以分为最大优先级队列和最小优先级队列。
优先级队列的概念和用途书上已经写的很清楚了,我就不再打一遍了。直接写出具体实现。
在实现前先说几点:
1.上一章说过,堆的length和heapsize要区分清楚,这一章的优先级队列里就用到了。
2.优先级队列用到了上一章的一些函数比如MaxHeapify(),不记得的可以复习下上一章。
以下是代码及讲解(此处实现的是最大优先级队列):
// 堆应用之优先级队列
// Tanky Woo
// Blog: www.WuTianQi.com
#include
using namespace std;
const int INF = 999999;
/////////////////////////////////////////////////////////
////////////// 以下代码在堆排序中已讲解过 ///////////////
void MaxHeapify(int *a, int i, int len)
{
int lt = 2*i, rt = 2*i+1;
int largest;
if(lt <= len && a[lt] > a[i])
largest = lt;
else
largest = i;
if(rt <= len && a[rt] > a[largest])
largest = rt;
if(largest != i)
{
int temp = a[i];
a[i] = a[largest];
a[largest] = temp;
MaxHeapify(a, largest, len);
}
}
void BuildMaxHeap(int *a, int size)
{
for(int i=size/2; i>=1; --i)
MaxHeapify(a, i, size);
}
void PrintArray(int data[], int size)
{
for (int i=1; i<=size; ++i)
cout < 1 &&a;[i/2] < a[i])
{
int temp = a[i];
a[i] = a[i/2];
a[i/2] = temp;
i /= 2;
}
}
// 插入关键字为key的元素
void MaxHeapInsert(int *a, int key, int &heapsize;)
{
++heapsize;
a[heapsize] = -INF;
HeapIncreaseKey(a, heapsize, key);
}
int main()
{
int len, heapsize;
int arr[100] = {0, 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1};
// 区别len 和 heapsize
// heapsize是堆的大小,而len是初始数组的总大小。
len = heapsize = 12;
// 首先建堆
BuildMaxHeap(arr, len);
cout << "建堆后: " << endl;
PrintArray(arr, len);
// 使用HeapMaximum
cout << "当前最大的元素是: " << endl;
cout << HeapMaximum(arr) << endl << endl;
// 使用HeapExtractMax
cout << "使用HeapExtractMax后: " << endl;
HeapExtractMax(arr,heapsize);
PrintArray(arr, heapsize);
// 再次使用HeapExtractMax
cout << "再次使用HeapExtractMax后: " << endl;
HeapExtractMax(arr,heapsize);
PrintArray(arr, heapsize);
// 使用HeapIncreaseKey
cout << "使用HeapIncreaseKey后: " << endl;
HeapIncreaseKey(arr, 2, 15);
PrintArray(arr, heapsize);
// 使用MaxHeapInsert
cout << "使用MaxHeapInsert后: " << endl;
MaxHeapInsert(arr, 28, heapsize);
PrintArray(arr, heapsize);
}
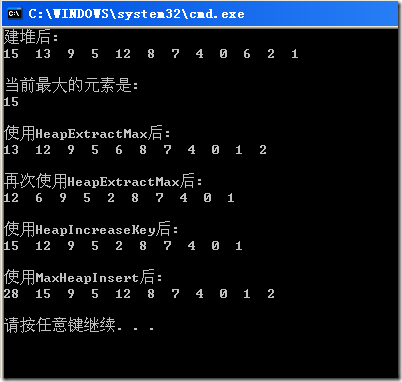
以下是运行结果:
看上图的结果:
在第二次使用HeapExtractMax后,把第二个数字即6设为15,更新后,结果就是HeapIncreaseKey的输出。