这篇博客是从旧博客 WordPress 迁移过来,内容可能存在转换异常。
插入结点用到了上一次BST的插入函数(做了一点添加),并且在此基础上增加了保持红黑性质的调整函数。
还是先看看插入函数:
void RBTreeInsert(RBTree &T;, int k)
{
//T->parent->color = BLACK;
Node *y = NULL;
Node *x = T;
Node *z = new Node;
z->key = k;
z->lchild = z->parent = z->rchild = NULL;
while(x != NULL)
{
y = x;
if(k < x->key)
x = x->lchild;
else
x = x->rchild;
}
z->parent = y;
if(y == NULL)
{
T = z;
T->parent = NULL;
T->parent->color = BLACK;
}
else
if(k < y->key)
y->lchild = z;
else
y->rchild = z;
z->lchild = NULL;
z->rchild = NULL;
z->color = RED;
RBInsertFixup(T, z);
}
和上一次的BST基本没区别,只是添加了对新加结点z的颜色和子节点的处理。
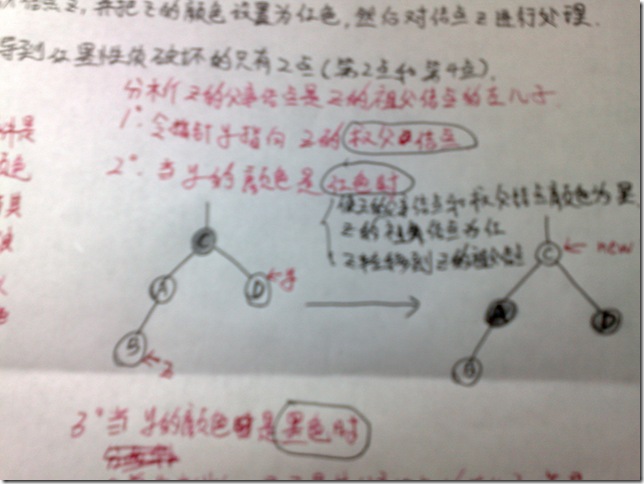
这里把z的颜色设置为红色,然后进行处理。
问:考虑为何把z的颜色设置为红色?
答:个人认为如果设置为黑色,则破坏了性质五,而性质五关于黑高度的问题,涉及到了整棵树,全局性难以把握,所以这里设置为红色,虽然破坏了性质4,然是相对破坏性质5来说,更容易恢复红黑性质。大家如果有不同的想法,也可以留言谈谈。
接下来,就是对整棵树的调整了。
答:考虑插入z结点后,破坏的哪几条红黑性质?
答:破坏了性质2和性质4.
5条红黑性质要熟记,我这里再贴出来:
- 每个结点或是红色,或是是黑色。
- 根结点是黑的。
- 所有的叶结点(NULL)是黑色的。(NULL被视为一个哨兵结点,所有应该指向NULL的指针,都看成指向了NULL结点。)
- 如果一个结点是红色的,则它的两个儿子节点都是黑色的。
- 对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
所以我们要做的就是恢复性质2和性质4.
先来看看具体实现的代码(这里只贴出部分代码):
void RBInsertFixup(RBTree &T;, Node *z)
{
while(z->parent->color == RED)
{
if(z->parent == z->parent->parent->lchild)
{
Node *y = z->parent->parent->rchild;
//////////// Case1 //////////////
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
////////////// Case 2 //////////////
if(z == z->parent->rchild)
{
z = z->parent;
LeftRotate(T, z);
}
////////////// Case 3 //////////////
z->parent->color = BLACK;
z->parent->parent->color = RED;
RightRotate(T, z->parent->parent);
}
}
else
{
///////////////////////
}
}
T->color = BLACK;
}
分三种情况,在代码中已用Case 1, Case 2, Case 3标记出。
大致说下判断情况:
1.首先让一个指针y指向z的叔父结点(z是要删除的结点)。
2.如果y的颜色是红色,Case 1。则使z的父亲结点和叔父结点的颜色改为黑,z的祖父结点颜色改为红。然后让z转移到z的祖父结点。
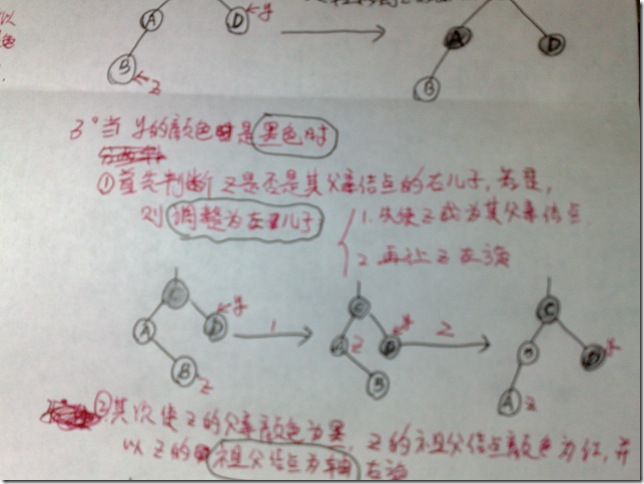
3.当y的颜色是黑色时,
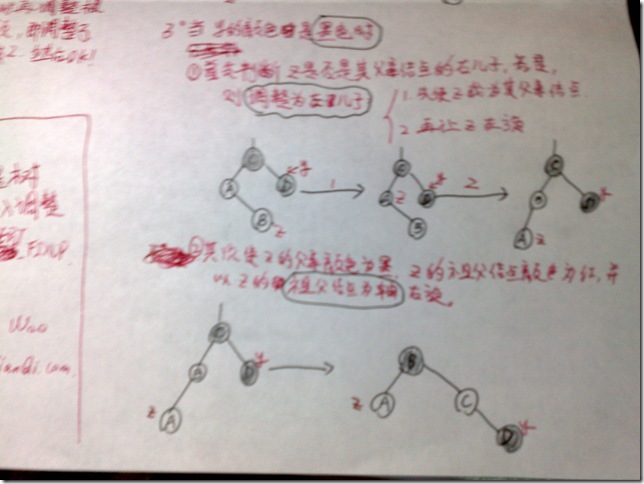
①.首先判断z是否是其父亲结点的右儿子,若是,则调整为左儿子(用旋转)。
②.其次使z的父亲结点颜色为黑,z的祖父结点颜色为红,并以z的祖父结点为轴右旋。
具体我还是在草稿纸上画出。。。(可怜买不起数码相机,只能用手机拍了。。。)
(弱弱的问一句,看见网上有很多朋友做的一些代码讲解图很给力,不知道大家有什么软件吗?求推荐。。。)
以下是插入的完整代码:
void RBInsertFixup(RBTree &T;, Node *z)
{
while(z->parent->color == RED)
{
if(z->parent == z->parent->parent->lchild)
{
Node *y = z->parent->parent->rchild;
//////////// Case1 //////////////
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
////////////// Case 2 //////////////
if(z == z->parent->rchild)
{
z = z->parent;
LeftRotate(T, z);
}
////////////// Case 3 //////////////
z->parent->color = BLACK;
z->parent->parent->color = RED;
RightRotate(T, z->parent->parent);
}
}
else
{
Node *y = z->parent->parent->lchild;
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
if(z == z->parent->lchild)
{
z = z->parent;
RightRotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
LeftRotate(T, z->parent->parent);
}
}
}
T->color = BLACK;
}
void RBTreeInsert(RBTree &T;, int k)
{
//T->parent->color = BLACK;
Node *y = NULL;
Node *x = T;
Node *z = new Node;
z->key = k;
z->lchild = z->parent = z->rchild = NULL;
while(x != NULL)
{
y = x;
if(k < x->key)
x = x->lchild;
else
x = x->rchild;
}
z->parent = y;
if(y == NULL)
{
T = z;
T->parent = NULL;
T->parent->color = BLACK;
}
else
if(k < y->key)
y->lchild = z;
else
y->rchild = z;
z->lchild = NULL;
z->rchild = NULL;
z->color = RED;
RBInsertFixup(T, z);
}
下一篇是关于红黑树的删除。
Tanky Woo 标签: 红黑树,Red Black Tree