这篇博客是从旧博客 WordPress 迁移过来,内容可能存在转换异常。
建议先看看前言:http://www.wutianqi.com/?p=2298
这一章的内容很简单,基本都是一些概念。
第i个顺序统计量:在一个由n个元素组成的集合中,第i个顺序统计量(order statistic)是该集合中第i小的元素。
最小值是第1个顺序统计量(i=1)
最大值是第n个顺序统计量(i=n)
中位数:一个中位数(median)是它所在集合的“中点元素”,当n为奇数时,i=(n+1)/2,当n为偶数是,中位数总是出现在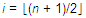 (下中位数)和
(下中位数)和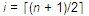 (上中位数)。
(上中位数)。
找最大值/最小值问题,通过比较n-1次可以得出结果。
MINIMUM(_A_)
1 _min_ ← _A_[1]
2 **for** _i_ ← 2 **to** _length_[_A_]
3 **do if** _min_ > _A_[_i_]
4 **then** _min_ ← _A_[_i_]
5 **return** _min_
如果要同时找出最大值和最小值,则比较次数最少并不是2*n-2,而是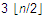 ,我们可以将一对元素比较,然后把较大者于max比较,较小者与min比较,这样就只需要
,我们可以将一对元素比较,然后把较大者于max比较,较小者与min比较,这样就只需要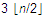 。
。
如果是一般的选择问题,即找出一段序列第i小的数,看起来要比找最大值或最小值要麻烦,其实两种问题的渐进时间都是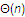 。
。
首先看看这个强悍的伪代码:
RANDOMIZED-SELECT(_A_, _p_, _r_, _i_)
1 **if** _p_ = _r_
2 **then return** _A_[_p_]
3 _q_ ← RANDOMIZED-PARTITION(_A_, _p_, _r_)
4 _k_ ← _q_ - _p_ + 1
5 **if** _i_ = _k_ ▹ the pivot value is the answer
6 **then return** _A_[_q_]
7 **elseif** _i_ < _k_
8 **then return** RANDOMIZED-SELECT(_A_, _p_, _q_ - 1, _i_)
9 **else return** RANDOMIZED-SELECT(_A_, _q_ + 1, _r_, _i_ - _k_)
这个算法利用了随机化的Partition算法,这个实在第七章的随机化快排中讲到:http://www.wutianqi.com/?p=2368,不记得的可以先复习下前面的快排。
这个随机化的选择算法返回数组A[p..r]中第i小的元素。
具体实现如下:
/*
Author: Tanky Woo
Blog: www.WuTianQi.com
About: 《算法导论》第9章 查找序列第i小的数字
*/
#include
#include
using namespace std;
int Partition(int *arr, int beg, int end)
{
int sentinel = arr[end];
int i = beg-1;
for(int j=beg; j<=end-1; ++j)
{
if(arr[j] <= sentinel)
{
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i+1], arr[end]);
return i+1;
}
int RandomPartition(int *arr, int beg, int end)
{
int i = beg + rand() % (end-beg+1);
swap(arr[i], arr[end]);
return Partition(arr, beg, end);
}
int RandomSelect(int *a, int p, int r, int i)
{
if(p == r)
return a[p];
int q = Partition(a, p, r);
int k = q-p+1;
if(i == k)
return a[q];
else if(i < k)
return RandomSelect(a, p, q-1, i);
else
return RandomSelect(a, q+1, r, i-k);
}
int main()
{
int a[] = {0, 89, 100, 21, 5, 2, 8, 33, 27, 63};
int num = 9;
int ith;
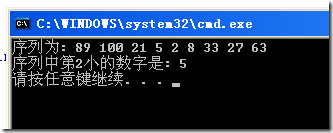
cout << "序列为: ";
for(int i=1; i<=num; ++i)
cout << a[i] << " ";
cout << endl;
ith = RandomSelect(a, 1, num, 2);
cout << "序列中第2小的数字是: " << ith << endl;
getchar();
return 0;
}
在(89, 100, 21, 5, 2, 8, 33, 27, 63)中查找第二小的数字是5.
该算法的平均情况性能较好,并且又是随机化的,所有没有哪一种特别的输入会导致最坏情况发生。
本文连接:http://www.wutianqi.com/?p=2395 欢迎大家互相讨论。