这篇博客是从旧博客 WordPress 迁移过来,内容可能存在转换异常。
建议先看看前言:http://www.wutianqi.com/?p=2298
这一章把前面三篇的代码总结起来,然后推荐一些网上红黑树的优秀讲解资源。
代码:
/*
* Author: Tanky Woo
* Blog: www.WuTianQi.com
* Description: 《算法导论》第13章 Red Black Tree
*/
#include
//#define NULL 0
using namespace std;
const int RED = 0;
const int BLACK = 1;
// ①
typedef struct Node{
int color;
int key;
Node *lchild, *rchild, *parent;
}Node, *RBTree;
static Node NIL = {BLACK, 0, 0, 0, 0};
#define NULL (&NIL;)
// ②
Node * RBTreeSearch(RBTree T, int k)
{
if(T == NULL || k == T->key)
return T;
if(k < T->key)
return RBTreeSearch(T->lchild, k);
else
return RBTreeSearch(T->rchild, k);
}
/*
BSNode * IterativeRBTreeSearch(RBTree T, int k)
{
while(T != NULL && k != T->key)
{
if(k < T->lchild->key);
x = T->lchild;
else
x = T->rchild;
}
return x;
}
*/
// ③
Node * RBTreeMinimum(RBTree T)
{
while(T->lchild != NULL)
T = T->lchild;
return T;
}
Node * RBTreeMaximum(RBTree T)
{
while(T->rchild != NULL)
T = T->rchild;
return T;
}
// ④
Node *RBTreeSuccessor(Node *x)
{
if(x->rchild != NULL)
return RBTreeMinimum(x->rchild);
Node *y = x->parent;
while(y != NULL && x == y->rchild)
{
x = y;
y = y->parent;
}
return y;
}
void LeftRotate(RBTree &T;, Node *x)
{
Node *y = x->rchild;
x->rchild = y->lchild;
if(y->lchild != NULL)
y->lchild->parent = x;
y->parent = x->parent;
if(x->parent == NULL)
T = y;
else
{
if(x == x->parent->lchild)
x->parent->lchild = y;
else
x->parent->rchild = y;
}
y->lchild = x;
x->parent = y;
}
void RightRotate(RBTree &T;, Node *x)
{
Node *y = x->rchild;
x->rchild = y->lchild;
if(y->lchild != NULL)
y->lchild->parent = x;
y->parent = x->parent;
if(x->parent == NULL)
T = y;
else
{
if(x == x->parent->lchild)
x->parent->lchild = y;
else
x->parent->rchild = y;
}
y->lchild = x;
x->parent = y;
}
// ⑤
void RBInsertFixup(RBTree &T;, Node *z)
{
while(z->parent->color == RED)
{
if(z->parent == z->parent->parent->lchild)
{
Node *y = z->parent->parent->rchild;
//////////// Case1 //////////////
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
////////////// Case 2 //////////////
if(z == z->parent->rchild)
{
z = z->parent;
LeftRotate(T, z);
}
////////////// Case 3 //////////////
z->parent->color = BLACK;
z->parent->parent->color = RED;
RightRotate(T, z->parent->parent);
}
}
else
{
Node *y = z->parent->parent->lchild;
if(y->color == RED)
{
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent;
}
else
{
if(z == z->parent->lchild)
{
z = z->parent;
RightRotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
LeftRotate(T, z->parent->parent);
}
}
}
T->color = BLACK;
}
void RBTreeInsert(RBTree &T;, int k)
{
//T->parent->color = BLACK;
Node *y = NULL;
Node *x = T;
Node *z = new Node;
z->key = k;
z->lchild = z->parent = z->rchild = NULL;
while(x != NULL)
{
y = x;
if(k < x->key)
x = x->lchild;
else
x = x->rchild;
}
z->parent = y;
if(y == NULL)
{
T = z;
T->parent = NULL;
T->parent->color = BLACK;
}
else
if(k < y->key)
y->lchild = z;
else
y->rchild = z;
z->lchild = NULL;
z->rchild = NULL;
z->color = RED;
RBInsertFixup(T, z);
}
// ⑤
void RBDeleteFixup(RBTree &T;, Node *x)
{
while(x != T && x->color == BLACK)
{
if(x == x->parent->lchild)
{
Node *w = x->parent->rchild;
///////////// Case 1 /////////////
if(w->color == RED)
{
w->color = BLACK;
x->parent->color = RED;
LeftRotate(T, x->parent);
w = x->parent->rchild;
}
///////////// Case 2 /////////////
if(w->lchild->color == BLACK && w->rchild->color == BLACK)
{
w->color = RED;
x = x->parent;
}
else
{
///////////// Case 3 /////////////
if(w->rchild->color == BLACK)
{
w->lchild->color = BLACK;
w->color = RED;
RightRotate(T, w);
w = x->parent->rchild;
}
///////////// Case 4 /////////////
w->color = x->parent->color;
x->parent->color = BLACK;
w->rchild->color = BLACK;
LeftRotate(T, x->parent);
x = T;
}
}
else
{
Node *w = x->parent->lchild;
if(w->color == RED)
{
w->color = BLACK;
x->parent->color = RED;
RightRotate(T, x->parent);
w = x->parent->lchild;
}
if(w->lchild->color == BLACK && w->rchild->color == BLACK)
{
w->color = RED;
x = x->parent;
}
else
{
if(w->lchild->color == BLACK)
{
w->rchild->color = BLACK;
w->color = RED;
LeftRotate(T, w);
w = x->parent->lchild;
}
w->color = x->parent->color;
x->parent->color = BLACK;
w->lchild->color = BLACK;
RightRotate(T, x->parent);
x = T;
}
}
}
x->color = BLACK;
}
Node* RBTreeDelete(RBTree T, Node *z)
{
Node *x, *y;
// z是要删除的节点,而y是要替换z的节点
if(z->lchild == NULL || z->rchild == NULL)
y = z; // 当要删除的z至多有一个子树,则y=z;
else
y = RBTreeSuccessor(z); // y是z的后继
if(y->lchild != NULL)
x = y->lchild;
else
x = y->rchild;
// 无条件执行p[x] = p[y]
x->parent = y->parent; //如果y至多只有一个子树,则使y的子树成为y的父亲节点的子树
if(y->parent == NULL) // 如果y没有父亲节点,则表示y是根节点,词典其子树x为根节点
T = x;
else if(y == y->parent->lchild)
// 如果y是其父亲节点的左子树,则y的子树x成为其父亲节点的左子树,
// 否则成为右子树
y->parent->lchild = x;
else
y->parent->rchild = x;
if(y != z)
z->key = y->key;
if(y->color == BLACK)
RBDeleteFixup(T, x);
return y;
}
void InRBTree(RBTree T)
{
if(T != NULL)
{
InRBTree(T->lchild);
cout << T->key << " ";
InRBTree(T->rchild);
}
}
void PrintRBTree(RBTree T)
{
if(T != NULL)
{
PrintRBTree(T->lchild);
cout << T->key << ": ";
// 自身的颜色
if(T->color == 0)
cout << " Color: RED ";
else
cout << " Color: BLACK ";
// 父亲结点的颜色
if(T == NULL)
cout << " Parent: BLACK ";
else
{
if(T->color == 0)
cout << " Parent: RED ";
else
cout << " Parent: BLACK ";
}
// 左儿子结点的颜色
if(T->lchild == NULL)
cout << " Lchild: BLACK ";
else
{
if(T->lchild->color == 0)
cout << " Lchild: RED ";
else
cout << " Lchild: BLACK ";
}
// 右儿子结点的颜色
if(T->rchild == NULL)
cout << " Rchild: BLACK ";
else
{
if(T->rchild->color == 0)
cout << " Rchild: RED ";
else
cout << " Rchild: BLACK ";
}
cout << endl;
PrintRBTree(T->rchild);
}
}
int main()
{
int m;
RBTree T = NULL;
for(int i=0; i<9; ++i)
{
cin >> m;
RBTreeInsert(T, m);
cout << "在红黑树中序查找:";
InRBTree(T);
cout << endl;
}
PrintRBTree(T);
cout << "删除根节点后:";
RBTreeDelete(T, T);
InRBTree(T);
}
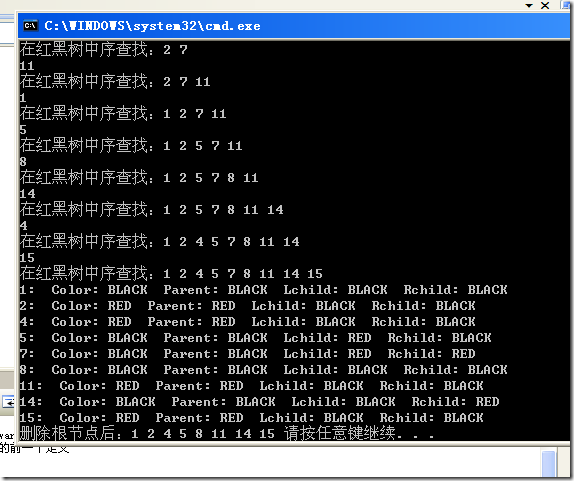
截图如图:
如图显示,这里用到了书上图13-4.可以看到,结点1, 5, 7, 8, 14是黑结点.和图13-4显示一样.
另外,我在学习红黑树的过程中,在网上发现了几个不错的资料,这里给大家推荐下:
天枰座的唐风朋友的:
http://liyiwen.iteye.com/blog/345800
http://liyiwen.iteye.com/blog/345799
wangdei的红黑树算法,附AVL树的比较:
http://wangdei.iteye.com/blog/236157
July的红黑树算法层层剖析与逐步实现:
[**1、教你透彻了解红黑树**](http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx)
[**2、红黑树算法的实现与剖析**](http://blog.csdn.net/v_JULY_v/archive/2010/12/31/6109153.aspx)
[**3、红黑树的c源码实现与剖析**](http://blog.csdn.net/v_JULY_v/archive/2011/01/03/6114226.aspx)
[**4、一步一图一代码,R-B Tree**](http://blog.csdn.net/v_JULY_v/archive/2011/01/09/6124989.aspx)
[**5、红黑树插入和删除结点的全程演示**](http://blog.csdn.net/v_JULY_v/archive/2011/03/28/6284050.aspx)
[**6、红黑树的c++完整实现源码**](http://blog.csdn.net/v_JULY_v/archive/2011/03/29/6285620.aspx)
感谢上面的朋友写的这么好的分析文章。