第十四章我想放在后面再看,先搁下。希望大家总结的一些文章也能向我推荐下,大家互相学习。
首先,还是建议看看前言:http://www.wutianqi.com/?p=2298
其次,阿门,感谢老天送给了我们这么一本圣经,看了这一章,再次感受到了《算法导论》分析问题的精辟,强悍的魅力。Orz, Orz,各种Orz。
这一章讲的是动态规划,学算法的朋友,尤其是搞ACM的,对这个策略一定非常熟悉,所以这个算法网上的分析讲解教程也是铺天盖地,大家可以多搜几篇学习学习。
动态规划(Dynamic Programming,简称DP)是通过组合子问题的解来解决问题的。
注意这里的programming不是指编程,而是指一种规划。
因为DP用的太广泛了,并且书上也花了很大的篇幅来讲这一章,所以我也准备把这一章分几篇来总结,并且我不按照书上的顺序来总结,也不会全部用书上的例子。
这一章首先给出一些基础的概念,然后给出一个最基础入门的DP问题,三角形求值问题。
DP适用于子问题不是独立的情况,这样如果用分治法,也会作许多重复的工作,而DP只对子问题求解一次,将其结果保存在一张表中,从而避免了每次遇到各个子问题时重新计算的情况。
比较分治法于动态规划的区别:
分治法:将问题划分为一些独立的子问题,递归的求解各子问题,然后合并子问题的解而得到原问题的解。
eg.
MERGE-SORT(_A_, _p_, _r_)
1 **if** _p_ < _r_
2 **then** _q_ ← |(_p_ + _r_)/2|
3 MERGE-SORT(_A_, _p_, _q_)
4 MERGE-SORT(_A_, _q_ + 1, _r_)
5 MERGE(_A_, _p_, _q_, _r_)
**动态规划**:适用于子问题**不是独立**的情况,也就是各子问题包含**公共的子子问题**,鉴于会重复的求解各子问题,DP对每个问
题**只求解一遍**,将其**保存在一张表**中,从而避免重复计算。
DP算法的设计可以分为四个步骤:
①.描述最优解的结构。
②.递归定义最优解的值。
③.按自底而上的方式计算最优解的值。
④.由计算出的结果创造一个最优解。
下面来看看三角形求值这个问题:
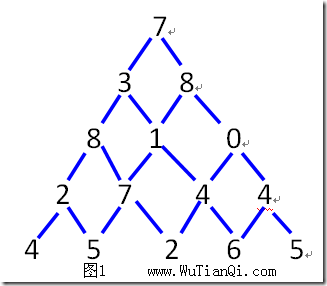
将一个由N行数字组成的三角形,如图所以,设计一个算法,计算出三角形的由顶至底的一条路径,使该路径经过的数字总和最大。
这是在我见过的DP题目中,算是最简单的了,我相信就算没有学过DP的也会。
将上图转化一下:
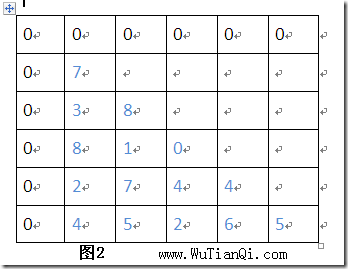
假设上图用map[][]数组保存。
令f[i][j]表示从顶点(1, 1)到顶点(i, j)的最大值。
则可以得到状态转移方程:
f[i][j] = max(f[i+1][j], f[i+1][j+1]) + map[i][j]
此题既适合自顶而下的方法做,也适合自底而上的方法,
当用自顶而下的方法做时,最后要在在最后一列数中找出最大值,
而用自底而上的方法做时,f[1][1]即为最大值。
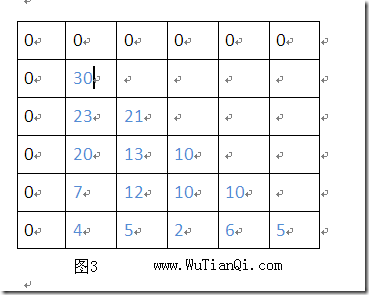
所以我们将图2根据状态转移方程可以得到图3:
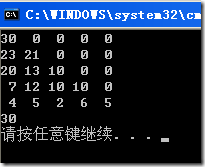
最大值是30.
很简单的DP题,代码如下:
/*
Author: Tanky Woo
Blog: www.WuTianQi.com
Description: 动态规划之三角形求值问题
*/
#include
using namespace std;
int map[6][6] =
{
{0, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 0, 0},
{0, 3, 8, 0, 0, 0},
{0, 8, 1, 0, 0, 0},
{0, 2, 7, 4, 4, 0},
{0, 4, 5, 2, 6, 5}
};
int f[6][6];
int _max(int a, int b)
{
if(a >= b)
return a;
return b;
}
int main()
{
memset(f, 0, sizeof(f));
for(int i=0; i<6; ++i)
f[5][i] = map[5][i];
for(int i=4; i>=1; --i)
for(int j=1; j<=i; ++j)
f[i][j] = _max(f[i+1][j], f[i+1][j+1]) + map[i][j];
for(int i=1; i<=5; ++i)
{
for(int j=1; j<=5; ++j)
{
cout.width(2);
cout << f[i][j] << " ";
}
cout << endl;
}
cout << f[1][1] << endl;
}
结果如图:
下一篇会将装配线的调度。