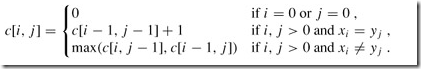这篇博客是从旧博客 WordPress 迁移过来,内容可能存在转换异常。
建议先看看前言:http://www.wutianqi.com/?p=2298
这个案例也比较简单,最长公共子序列(LCS),网上的分析非常多,给力啊!
按照上一篇总结所说的,找状态转移方程:
所以按照所给方程,写代码的工作就非常非常简单轻松了:
/*
Author: Tanky Woo
Blog: www.WuTianQi.com
About: 《算法导论》15.4 最长公共自序列(LCS)
*/
#include
using namespace std;
char b[20][20];
int c[20][20];
char x[20], y[20];
void LCS()
{
int m = strlen(x+1);
int n = strlen(y+1);
for(int i=1; i<=m; ++i)
c[i][0] = 0;
for(int j=1; j<=n; ++j)
c[0][j] = 0;
for(int i=1; i<=m; ++i)
for(int j=1; j<=n; ++j)
{
if(x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = '\\'; // 注意这里第一个\\是转移字符,代表\
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = '|';
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = '-';
}
}
}
void printLCS(int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == '\\')
{
printLCS(i-1, j-1);
cout << x[i] << " ";
}
else if(b[i][j] == '|')
printLCS(i-1, j);
else
printLCS(i, j-1);
}
int main()
{
cout << "Input the array A:\n";
cin >> x+1;
cout << "Input the array B:\n";
cin >> y+1;
LCS();
printLCS(strlen(x+1), strlen(y+1));
}
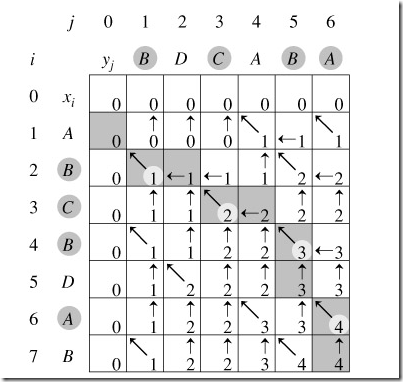
看书上图15-6的结果图:
又是一个给力的图,建议自己按照程序把这个图画出来.
另外,说到LCS,不得不说的是LIS(最长上升子序列),也是一个DP,我曾经总结过: