凸包:点集Q的凸包(convec hull)是一个最小的凸多边形P,满足Q中的所有点或者在P的边界上,或者在P的内部。
例如:
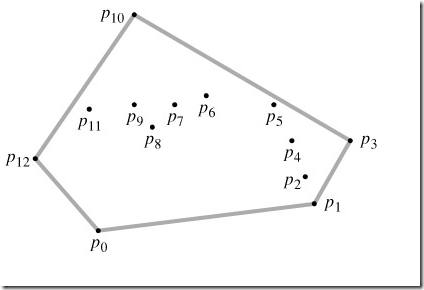
点集Q={p0, p1, …,p12}及其以灰色显示的凸包CH(Q)
这里介绍一种求凸包所包含点集的方法---Graham Scan。
这里在《算法导论》第33章计算几何学的第三节“寻找凸包”讲的很详细,还是以上图为例,看看凸包的建造过程:
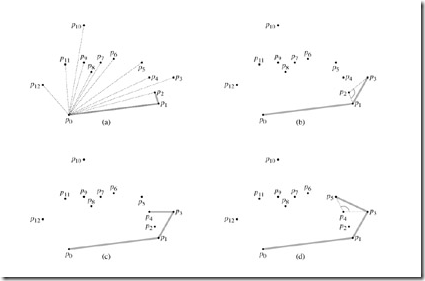
步骤1:如图(a),以y轴最低点为基点,找到基点p0。
步骤2:如图(a),以基点p0为一个坐标系的远点,求各点与基点p0的极角,并一次从小到大排序
步骤3:如图(b),按照顺序,每个点都要判断与其前面亮点构成的两条线段转向问题(左转还是右转?用叉积),这个具体看后面伪代码。
步骤4:依次下去,知道所有的点结束,就完成的凸包的寻找。
完整的图见《算法导论》P586~P587面。
这是《算法导论》上的伪代码:
GRAHAM-SCAN(_Q_)
1 let _p_0 be the point in _Q_ with the minimum _y_-coordinate,
or the leftmost such point in case of a tie
2 let 〈_p_1, _p_2, ..., _pm_〉 be the remaining points in _Q_,
sorted by polar angle in counterclockwise order around _p_0
(if more than one point has the same angle, remove all but
the one that is farthest from _p_0)
3 PUSH(_p_0, _S_)
4 PUSH(_p_1, _S_)
5 PUSH(_p_2, _S_)
6 **for** _i_ ← 3 **to** _m_
7 **do while** the angle formed by points NEXT-TO-TOP(_S_), TOP(_S_),
and _pi_ makes a nonleft turn
8 **do** POP(_S_)
9 PUSH(_pi, S_)
10 **return** _S_
可以看到步骤3,在伪代码中用Q保存凸包点集,每次按顺序从输入的点集P中取出一点P[i],与栈Q中最上面两点Q[top], Q[top-1]构成两条线段,若左转,则继续;否则将弹出栈顶的点Q[top],并再在栈中取一点Q[top-2],然后将P[i], Q[top-1], Q[top-2]继续比较,直至是左转~~~不好理解吧?还是看《算法导论》书上那图吧,神马讲解都是浮云,有图有真相才是王道。
理解后,看看这道题吧:
POJ 1113 Wall:http://poj.org/problem?id=1113
经典的凸包问题,这里就不做分析了,具体分析及代码在:http://www.wutianqi.com/?p=2613
另外,在学习凸包的过程中,在网上搜集到了两篇讲解的非常好的文章:
1.http://www.cnblogs.com/Booble/archive/2011/02/28/1967179.html
2.http://www.cnblogs.com/devymex/archive/2010/08/09/1795392.html
Tanky Woo 标签: Tanky Woo,Convec Hull,凸包